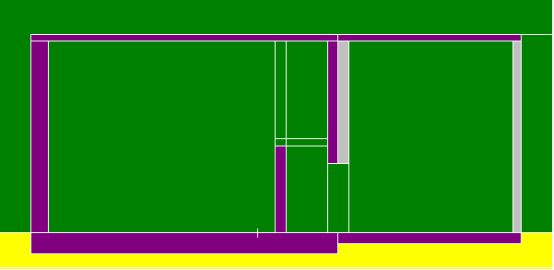
某带源实验室立面MCNP计算模型

公司设计团队针对某带源实验室的辐射剂量率水平做了程序模拟，根据现有屏蔽设计情况，分析了放射源位置与观测点剂量率的关系：

当放射源处于表中后两个位置时，相当于仅有迷路半墙作为屏蔽。此时，控制室门需采用屏蔽门。对比可知：放射源位置影响观测点处辐射剂量率水平，在一些极端位置，甚至会增加更多的项目投资预算，造成极大的经济代价。这也突显了专业屏蔽设计的重要性。

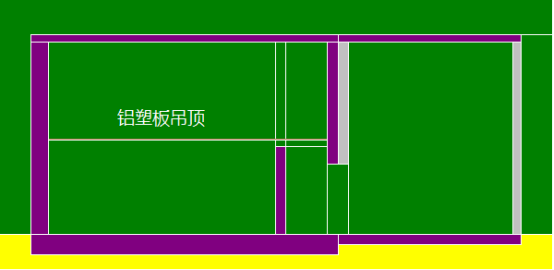
吊顶计算模型

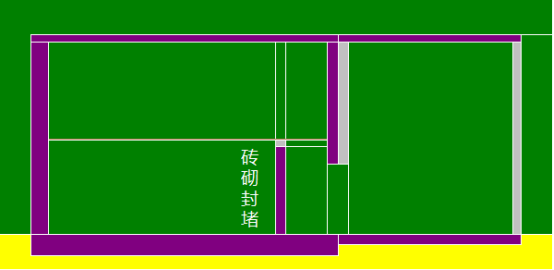
砖砌墙封堵模型

因原实验室上部存在较大的结构空间，从人因工程学角度考虑，为增加操作人员的舒适性，对实验室进行了吊顶设计。吊顶材料选用常规铝塑板，吊顶标高+3.00 m。通过程序模拟发现：吊顶后，因散射距离变短，观测点处剂量率水平有一定增加，可考虑砖砌墙进行适当屏蔽补偿。