背景介绍

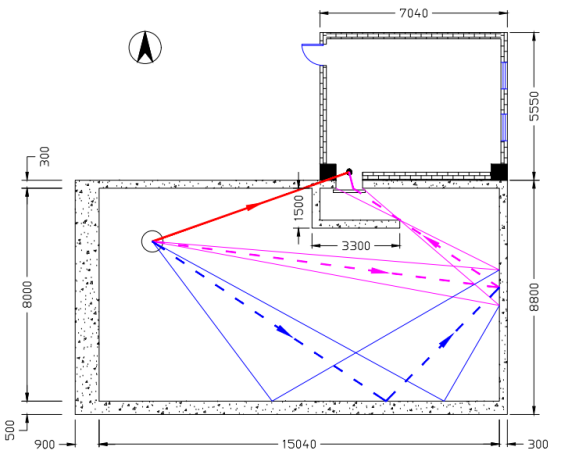
某操作¹³⁷Cs放射源的实验室(层高5.5 m)，活度11.1 GBq；总平图如下：

建立直角坐标系，以实验室内墙西北地坪角为原点。放射源坐标(2.00，-2.00，1.40)，单位m。计算控制室门洞后30 cm，距地标高1.40 m处的辐射水平。

计算方法(公式法)

⑴ 伽玛剂量率常数

¹³⁷Cs是纯β核素，其衰变子体^137mBa退激发光谱如下：

表1.1 ^137mBa退激光谱

注：能量吸收系数μ_en可通过《辐射防护手册 第一分册：辐射源与屏蔽》表C-1插值获得。

^137mBa弦能 y=n_iE_iμ_eni=2.3681×10^-5 MeV/cm，¹³⁷Cs→^137mBa衰变分支比为94.6%；伽玛剂量率常数：

                        K_γ=8.76×10³×3600×10⁶×94.6%×2.3681×10^-5/(4π×100²×33.73×2.083×10⁹)

                                 =8.0017×10^-8 (μGy·m²)/(GBq·h)

式中，8.76×10³ μGy/R是照射量-剂量转换系数，2.083×10⁹ R^-1是单位照射量在1 cm³标态空气中电离生成的离子对数，33.73 eV是每电离出一个离子对所需要吸收的能量。

⑵ 直射分量

① 关注点距离R

R=[(9.4-2)²+(0.6+2)²]^0.5=7.8435 m

② 混凝土厚度d

d=0.6/cos{tg^-1[(2+0.6)/(9.4-2)]}=0.6360 m

③ 积累因子B

B=A₁e^-α1μd+(1-A₁)e^-α2μd=26.5713

光子在混凝土中的线性衰减系数μ可通过《辐射防护手册 第一分册：辐射源与屏蔽》表5.7插值获得；系数A₁、α₁、α₂可通过同书表5.20插值获得。

④ 直射分量所致剂量当量率

H=ABK_γe^-μd/R²=0.0394μGy/h

⑶ 散射分量

估算散射分量重点在于散射路径地选取。一般而言，以初次散射后的散射光子能量作为整个散射光谱的代表，选取经历最少散射次数的路径作为散射分量为计算依据是偏安全的。

① 散射光子能量

低能辐射物理中，光子散射主要取决于康普顿作用，可根据以下公式计算散射光子能量：

E_γ=E₀/[1+E₀(1-cosθ_s)/m_ec²_]

其中，m_ec²是电子湮灭能量，0.511 MeV。θ_s是散射角，当入射光线、法线和出射光线三线共面时，θ_s=180°-(θ+θ₀)；非特殊情况可根据余弦定理求解：

cosθ_s=sinθsinθ₀cosφ-cosθcosθ₀

其中，θ为入射角，θ₀为出射角。

② 伽玛反照率

现行标准中也将该参数称为反散射系数，由于按康普顿散射考虑整个光子散射过程，故可根据如下经验公式计算反照率：

α_i=[C_iK(θ_s)×10²⁶+C′_i]/(1+cosθ₀/cosθ)

式中，K(θ_s)是康普顿微分散射截面，可通过Klein-Nishina公式计算得到；C_i和C′_i是与入射光子能量相关的流量反照率计算系数：

K(θ_s)=r₀²{(1+cos²θ_s)/[2+2a(1-cosθ_s)]}{1+[a(1-cosθ_s)]²/[(1+cos²θ_s)(1+a-acosθ_s)]}

其中，r₀是电子经典半径，2.818×10^-13cm；a≡E_0/mec²；入射光子能量区间为[0.1，10]，单位MeV时，C_i和C′_i取值分别如下： 

     lnC_i=-2.92+0.681×lnE₀+0.0111×(lnE₀)²-0.0413×(lnE₀)³

lnC′_i=-5.89+0.275×(E₀-3.25)²，0.1≤E₀＜1；

lnC′_i=-4.86+0.360×(E₀-2)²，1≤E₀＜2；

lnC′_i=-4.83+0.013E₀，2≤E₀＜10。

③ 墙面一次散射路径(洋红色)

a. 散射径迹几何

控制室门洞西侧(8.90，0，1.40)，东侧(9.90，0，1.40)，迷宫顶角(11.30，-1.20，1.40)；根据直线方程求解实验室东墙内壁三点坐标，分别为(15.04，-3.04，1.40)、(15.04，-4.00，1.40)、(15.04，-4.41，1.40)，由几何关系求解源点三角：θ′₁=4.6909°、θ′₂=7.5719°、θ′₃=10.4528°；其中，θ′₂与光线入射角θ′为内错角，散射光线出射角θ′₀与迷宫顶角、东墙内壁散射点相关：

                               θ′₀=tg^-1[(3.04-1.20)/(15.04-11.30)]=36.8134°

θ′_s=180°-36.8134°-7.5719°=135.6147°

散射面积ΔA与实验室东墙内壁三点相关，其宽度w=4.41-3.04=1.34 m，高度h=5.50 m，ΔA=17.6034 m²。

入射光径迹长R₁和散射光径迹长R₂、R₃分别可计算：

R₁=13.1924 m，R₂=6.6742 m，R₃=0.6694 m

b. 伽玛反照率

根据公式，可计算一次散射后，光子平均能量E_γ=0.2055 MeV，康普顿微分散射截面K(θ_s)=3.75×10^-26，剂量流量反照率α_d=0.0763。

c. 关注点散射剂量当量率

代入，可得：

                  H₁=AK_γ·ΔA·α_d·cosθ₀/[R₁²(R₂+R₃)²]=0.0425 μGy/h

其中，cosθ₀是剂量流量反照率换算剂量通量反照率的因子。

④ 其他主要路径

a. 墙面二次散射路径(蓝色)

                  H₂=AK_γ·ΔA₁·ΔA₂·α_d1·α_d2·cosθ₀₁·cosθ₀₂/[R′₁²R′₂²(R′₃+R′₄)²]

                          =0.0031 μGy/h

b. 楼板一次散射路径

                                    H₃=AK_γ·ΔA₃·α_d3·cosθ₀₃/(R″₁²·R″₂²)=0.7988 μGy/h

⑤ 迷宫优化

据前述计算，放射源通过楼板散射，因距离更近，其散射剂量较大；可根据实际情况考虑将迷宫半墙加筑至顶，或增加盖板，屏蔽来自楼板的散射。由于散射光子能量低于0.5 MeV，需根据《辐射防护手册 第一分册：辐射源与屏蔽》表5.20外推积累因子系数，误差很难得到保证；故以偏安全的保守估计，屏蔽透射系数计算按0.6616 MeV考虑：全墙和盖板时，楼板散射剂量当量率分别降为0.02172 μGy/h和0.03404 μGy/h。

⑷ 总剂量率

¹³⁷Cs放射源其他方向的散射因次数更多，到达关注点的通量密度更小，叠加到总剂量当量率的效果也越弱。因此，本计算结果中，总剂量当量率包好直射分量和3个散射分量。

迷宫半墙时，总剂量当量率为0.8838 μGy/h；

迷宫全墙时，总剂量当量率为0.1067 μGy/h；

迷宫盖板时，总剂量当量率为0.1191 μGy/h。

方法评价

显然，公式法计算关注点辐射剂量率水平存在较大局限性：过程参数多需内插或外推法求得，由此引入较多的额外误差；同时，散射路径的选择因人而异，以上种种，导致公式法计算结果误差范围较大，一般可保证不存在数量级差异。因此，公式法结果往往需要留有2～4倍的安全裕量，这也导致用公式法计算屏蔽厚度时，往往较实际情况偏保守，不利于辐射防护最优化的实施。