背景介绍
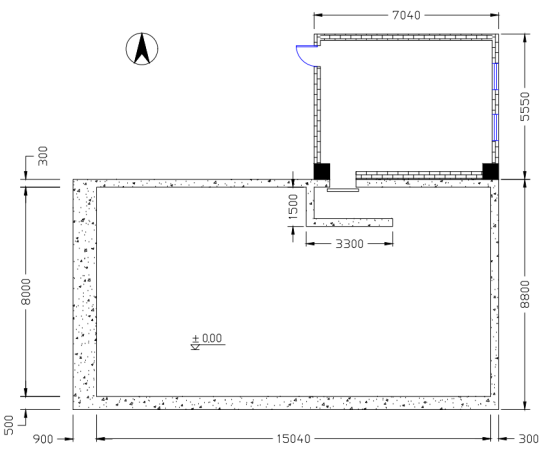
某操作137Cs放射源的实验室(层高5.50 m),活度11.1 GBq;总平图如下:
计算方法(蒙特卡罗方法)
蒙特卡罗方法又叫随机抽样法或统计实验方法,属于计算数学的一个分支。其基本思想是当所求问题的解是某个事件的概率,或是某个随机变量的数学期望,或是与概率或数学期望有关的量时;通过某种数值实验的方法得出该事件发生的频率,或该随机变量的若干具有观察值的算术平均值,并通过这样的研究来得到问题的解。
由于蒙特卡罗方法在解决粒子输运问题上的优越性,MCNP、EGS、MORSE以及FLUKA等蒙特卡罗程序也应运而生。其中,由美国洛斯阿拉莫斯国家实验室(Los-Alamos National Laboratory)开发的MCNP和由美国斯坦福直线加速器中心、日本高能物理国家实验室以及加拿大国家研究所联合开发的EGS4是目前应用较多并得到广泛验证的两种经典蒙特卡罗程序。
⑴ MCNP建模
本文计算坐标系与《某带源实验室辐射剂量率水平估算》相同,均以实验室西北地坪角为原点。MCNP建模如下:
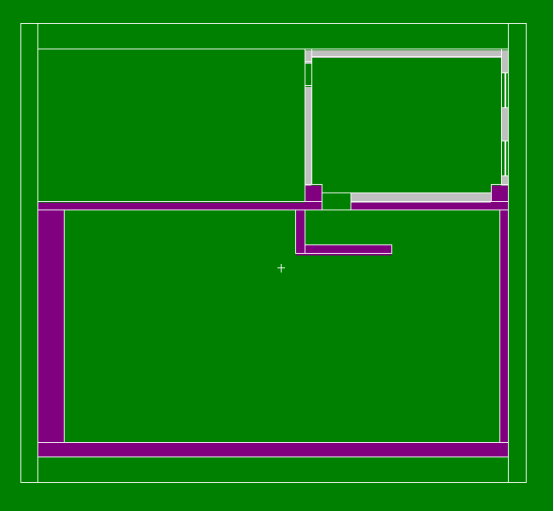
某带源实验室MCNP模型图
色标材料:
绿 色:空 气,密度:0.00122 g/cm3
紫 色:混凝土,密度:2.35 g/cm3
灰 色:页岩砖,密度:1.65 g/cm3
黄 色:泥 土,密度:1.46 g/cm3
淡蓝色:玻 璃,密度:2.50 g/cm3
深蓝色:铸铁皮,密度:7.85g/cm3
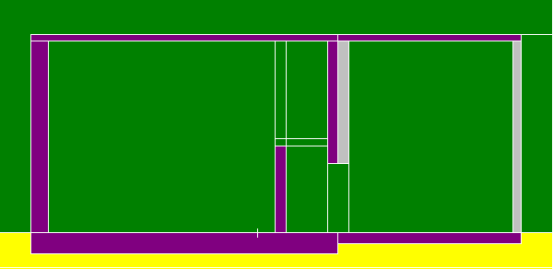
某带源实验室迷宫截面图
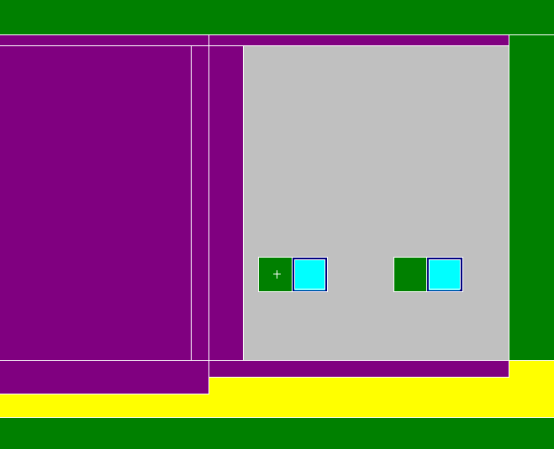
某带源实验室东侧墙剖面图
MCNP可实现精细化建模,在条件允许下,甚至可完成与计算关联性不大的控制室窗户的模型建立。
⑵ MCNP计算结果
由于MCNP程序属于蒙特卡罗方法的一种用于解决复杂几何结构的多粒子及多粒子耦合输运问题的程序包,是随20世纪国际原子能事业发展起来的可用于真实模拟多数物理过程的软件。具有结果收敛,自带方差等优点;因此,MCNP解决问题与实际非常符合,可享有很高的精度,其结果不受插值参数或径迹选择影响,可得到较为圆满的结果。
针对迷宫墙体建筑方案,MCNP可分别建模计算:

实验室迷宫盖板截面图
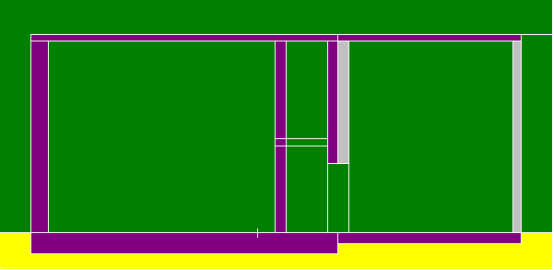
实验室迷宫全墙截面图
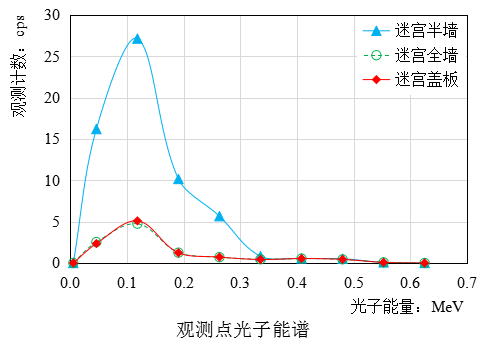
三种情况计算结果:
迷路墙方式 | 空气吸收剂量率:μGy/h | 误差倍数 H公式法/H程序法 | |
公式法 | MCNP | ||
半墙 | 0.884 | 0.125 | 7.07 |
全墙 | 0.107 | 0.027 | 4.41 |
盖板 | 0.119 | 0.027 | 3.95 |
通过DE-DF点值函数(各种剂量转换因子),MCNP还可将计算得出的光子通量密度转化为可用于不同评价目的的辐射量:
迷路墙方式 | 空气吸收剂量率 | 周围剂量当量率 | 小时有效剂量 |
半墙 | 0.125 μGy/h | 0.186 μSv/h | 0.155 μSv |
全墙 | 0.027 μGy/h | 0.038 μSv/h | 0.032 μSv |
盖板 | 0.027 μGy/h | 0.039 μSv/h | 0.032 μSv |